用Python实现斐波那契数列

斐波那契数列是一个经典的数学序列，它在计算机科学和算法设计中有着广泛的应用；本文将介绍如何使用Python编程语言实现斐波那契数列的四种方法。

1. 递归方法

递归算法是实现斐波那契数列的最简单方法。代码如下：

import time

def fibonacci_recursive(n):
    if n <= 1:
        return n
    else:
        return fibonacci_recursive(n-1) + fibonacci_recursive(n-2)

n = 40
start = time.time()
value = fibonacci_recursive(n)
print(f"第 {n} 项为 {value}\n耗时: {time.time() - start}")

程序运行结果

第 40 项为 102334155
耗时: 26.679578065872192

虽然递归算法简单易懂，但它的时间复杂度较高O(2n)，适合用于理解斐波那契数列的基本结构。

2. 迭代方法

迭代方法更高效，适合用于计算较大范围内的斐波那契数列。代码如下：

import time

def fibonacci_iterative(n):
    a, b = 0, 1
    for _ in range(n):
        a, b = b, a + b
    return a

n = 40
start = time.time()
value = fibonacci_iterative(n)
print(f"第 {n} 项为 {value}\n耗时: {time.time() - start}")

程序运行结果

第 40 项为 102334155
耗时: 0.0

该方法通过循环实现，时间复杂度为O(n)，比递归方法更为高效。

3. 动态规划方法

动态规划方法通过存储子问题的结果来提高效率，非常适合计算非常大的斐波那契数列。代码如下：

import time

def fibonacci_dynamic(n):
    fib = [0, 1]
    for i in range(2, n+1):
        fib.append(fib[i-1] + fib[i-2])
    return fib[n]

n = 40
start = time.time()
value = fibonacci_dynamic(n)
print(f"第 {n} 项为 {value}\n耗时: {time.time() - start}")

程序运行结果

第 40 项为 102334155
耗时: 0.0

这种方法的时间复杂度同样为O(n)，但其空间复杂度也为O(n)，适合用于需要快速计算结果的场景。

4. 使用通项公式

斐波那契数列的通项公式为：

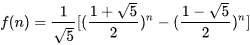
使用 Python实现如下：

import time
import math

def fibonacci_form(n):
    sqrt5 = math.sqrt(5)
    phi = (1 + sqrt5) / 2
    psi = (1 - sqrt5) / 2
    return int((phi**n - psi**n) / sqrt5 + 0.5)

n = 40
start = time.time()
value = fibonacci_form(n)
print(f"第 {n} 项为 {value}\n耗时: {time.time() - start}")

使用通项公式的时间复杂度为O(1)。